Herhangi bir sayı öbeğinde, sayıları oluşturan ilk rakamların aynı sıklıkla bulunmadığına hiç dikkat ettiniz mi? Aslına bakarsanız 1’den 9’a kadar olan rakamların, sayıların başlarında bulunma olasılıklarının eşit yani 9’da 1 olduğunu zannedersiniz. Fakat işin aslı öyle değildir. İlk başta çok tuhaf görünen ama gerçek olan bu olay, matematikçiler tarafından Benford Yasası olarak adlandırılır.
Benford Yasası Nedir?
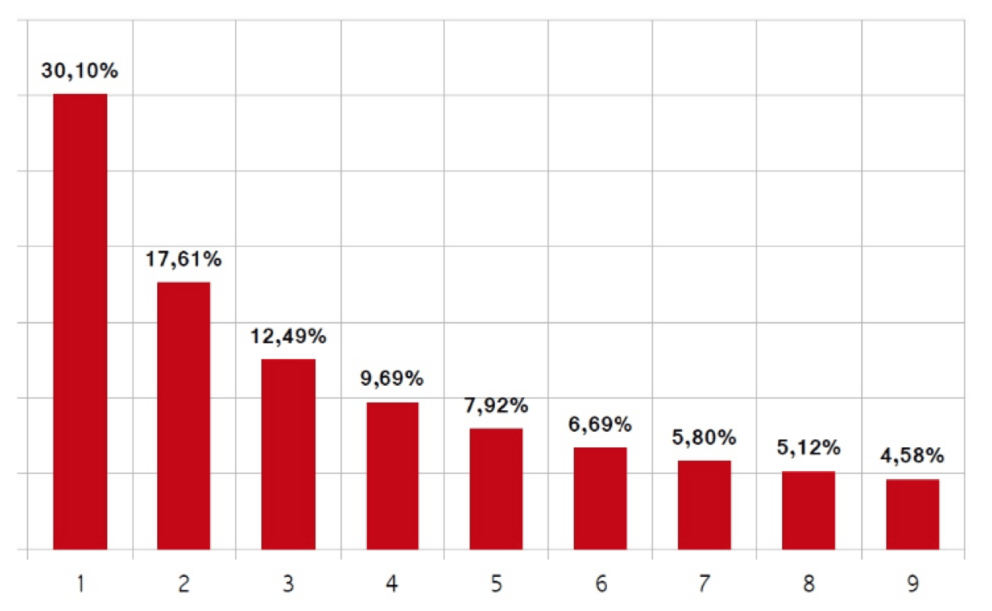
İlk olarak bu yasa 1881 yılında Simon Newcomb tarafından ortaya atılsa da, 1938 yılında fizikçi Frank Benford tekrar bu yasayı ortaya çıkarmış ve yasaya ismi konulmuştur. Benford Yasası, Newton’un Evrensel Kütle Çekimi Yasası gibi kabul görmüş bir kanun değildir. Ama yine de en sevdiğiniz şarkıdan tutun da, en sevdiğiniz spor dalının içinde bile bu yasaya rastlarsınız. Bu yasaya göre evrendeki sayıların %30,1’i 1 rakamı ile başlar. İstediğiniz bir sayı öbeğini kendiniz de inceleyebilirsiniz. Gerek herhangi bir şehirdeki daire fiyatları olsun, gerekse ülkelerin nüfusları, ya da vergi rakamları olsun. İlk hanesi hariç, geri kalan tüm rakamları atarsanız çok büyük bir sıklıkla bir şablona uyduğunu görürsünüz. 1’ler 2’lerden fazla, 2’ler 3’lerden fazla, 3’ler 4’lerden fazla çıkar ve bu böyle devam eder. Bu durum sadece birkaçında değil, büyük bir çoğunda görülmektedir. Aşağıdaki tabloda Benford Yasası’na göre rakamların ne sıklıkla bulundukları görülmektedir. Bu tabloya göre rakamlar büyüdükçe logaritmik açıyla da yüzde küçülmektedir.
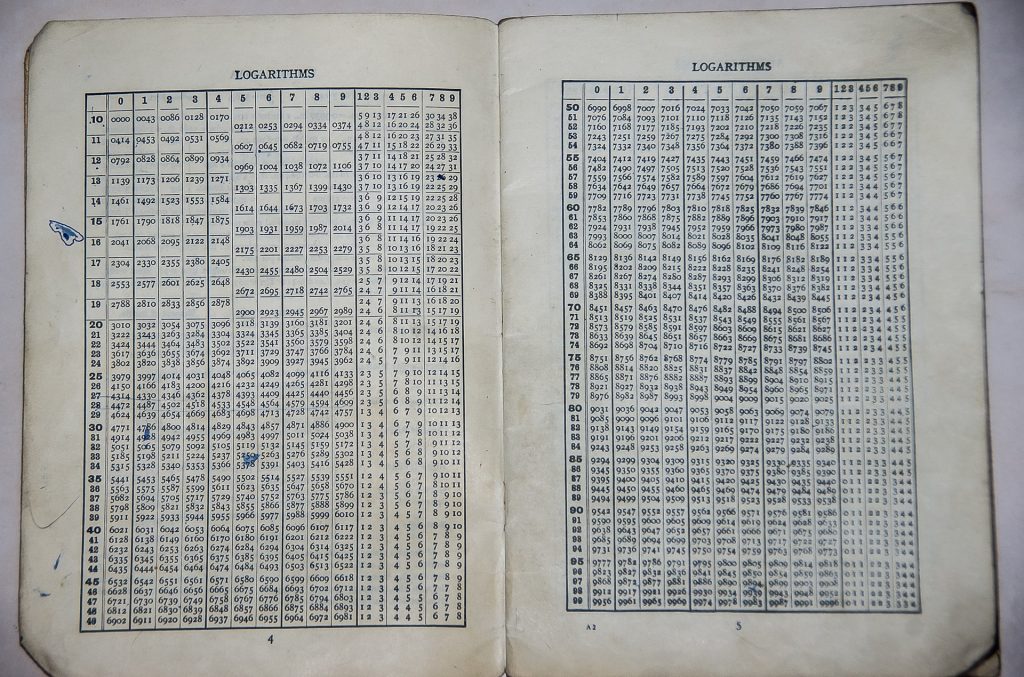
Benford’dan önce 1881’de matematikçi ve astronom Simon Newcomb, önceleri hesap makinesi yerine kullanılan logaritma kitaplarıyla çalışırken, ön sayfaların sonraki sayfalara göre daha çok yıprandığını görerek bu keşfi yaptı. Logaritma kitapları, ilk basamağı düşük olan sayıların logaritmaları ön sayfalarda ve ilk basamağı yüksek olan sayıların logaritmaları ise arka sayfalarda olacak şekilde yapılandırılmıştır. Logaritma kitaplarının da ilk sayfalarının arka sayfalara nispeten daha çok aşınmasından yola çıkarak, ilk basamağı düşük sayıların sayı içeren tablolarda daha sık görüldüğü kanısına varmıştır.
57 yıl sonra, 1938’de fizikçi Frank Benford aynı keşfi logaritma kitaplarıyla yaptı. Bu fenomenden büyülenerek, çok çeşitli alanlardan büyük miktarda veri topladı ve böylece öndeki basamaklar için bir logaritmik dağılım fonksiyonunun varlığını doğruladı.
Bununla birlikte, ne Benford ne de Newcomb savlarında matematiksel kanıt sağlayamadı. İlk kanıt, 1961’de R.Pinkham’dan geldi.
Benford Kanunun Nerelerde Kullanılır?
ABD’li bilim insanı Mark Nigrini, vergi beyannamelerinde ve bilançolarda yer alan rakamların sahte olmamak kaydıyla Benford yasalarına uygun olduğunu keşfetti. Yaklaşık 200.000 vergi iadesini inceledi ve aslında listelenen miktarların neredeyse üçte birinin bir ile başladığını buldu. Bu temelde, veri öbeklerini Benford yasasına uygun olup olmadığını için kontrol eden bir yazılım geliştirdi. Sadece ilk rakamlar değil, ikincisi de incelenir. Nigrini bu tekniği “dijital analiz” olarak adlandırıyor.
İlginç video paylaşımlarımızı izlemek için lütfen Youtube Kanalımıza abone olmayı ihmal etmeyin!